Epidemics spreading in space and time

24 August 2023

Julien Arino

Department of Mathematics & Data Science Nexus
University of Manitoba*

Canadian Centre for Disease Modelling
Canadian COVID-19 Mathematical Modelling Task Force
NSERC-PHAC EID Modelling Consortium (CANMOD, MfPH, OMNI/RÉUNIS)

* The University of Manitoba campuses are located on original lands of Anishinaabeg, Cree, Oji-Cree, Dakota and Dene peoples, and on the homeland of the Métis Nation.

Pathogens have been mobile for a while

It first began, it is said, in the parts of Ethiopia above Egypt, and thence descended into Egypt and Libya and into most of the King's country [Persia]. Suddenly falling upon Athens, it first attacked the population in Piraeus—which was the occasion of their saying that the Peloponnesians had poisoned the reservoirs, there being as yet no wells there—and afterwards appeared in the upper city, when the deaths became much more frequent.

Thucydides (c. 460 BCE - c. 395 BCE)

History of the Peloponnesian War

Outline

  • Mobility and the spread of infectious diseases
  • Formulating metapopulation models
  • Basic mathematical analysis
  • is not the panacea - An urban centre and satellite cities
  • Problems specific to metapopulations
  • Numerical investigations of large-scale systems

Mobility and the spread of infectious diseases

Mobility is complicated and drives disease spatialisation

Mobility is complicated:

  • Multiple modalities: foot, bicycle, personal vehicle, bus, train, boat, airplane
  • Various durations: trip to the corner shop commuting multi-day trip for work or leisure relocation, immigration or refuge seeking
  • Volumes are hard to fathom

And yet mobility drives spatio-temporal spread:

The Black Death: quick facts

  • First of the middle ages plagues to hit Europe
  • Affected Afro-Eurasia from 1346 to 1353
  • Europe 1347-1351
  • Killed 75–200M in Eurasia & North Africa
  • Killed 30-60% of European population

Plague control measures

  • Lazzarettos of Dubrovnik 1377 (30 days)
  • Quarantena of Venice 1448 (40 days)
  • Isolation of known or suspected cases as well as persons who had been in contact with them, at first for 14 days and gradually increased to 40 days
  • Improvement of sanitation: development of pure water supplies, garbage and sewage disposal, food inspection
  • .. Find and kill a snake, chop it into pieces and rub the various parts over swollen buboes. (Snake, synonymous with Satan, was thought to draw the disease out of the body as evil would be drawn to evil)

Pathogen spread has evolved with mobility

  • Pathogens travel along trade routes

  • In ancient times, trade routes were relatively easy to comprehend

  • With acceleration and globalization of mobility, things change

Fragmented jurisdictional landscape

  • Political divisions (jurisdictions): nation groups (e.g., EU), nations, provinces/states, regions, counties, cities..
  • Travel between jurisdictions can be complicated or impossible
  • Data is integrated at the jurisdicional level
  • Policy is decided at the jurisdictional level
  • Long range mobility is a bottom top top bottom process

Why mobility is important in the context of health

All migrants/travellers carry with them their "health history"
  • latent and/or active infections (TB, H1N1, polio)
  • immunizations (schedules vary by country)
  • health/nutrition practices (KJv)
  • treatment methods (antivirals)
Pathogens ignore borders and politics
  • antiviral treatment policies for Canada and USA
  • SARS-CoV-2 anyone?

SARS-CoV-1 (2002-2003)

Overall impact

  • Index case for international spread arrives HKG 21 February 2003

  • Last country with local transmission (Taiwan) removed from list 5 July 2003

  • 8273 cases in 28 countries

  • (Of these cases, 1706 were HCW)

  • 775 deaths (CFR 9.4%)

Polio spread 2002-2006. Pallansch & Sandhu, N Engl J Med 2006; 355:2508-2511

Formulating metapopulation models

General principles (1)

  • geographical locations (patches) in a set (city, region, country..)
  • Patches are vertices in a graph
  • Each patch contains compartments
    • individuals susceptible to the disease
      • individuals infected by the disease
      • different species affected by the disease
      • etc.

General principles (2)

  • Compartments may move between patches, with rate of movement of individuals from compartment from patch to patch
  • Movement instantaneous and no death during movement
  • , defines a digraph with arcs
  • Arc from to if , absent otherwise
  • compartments, so each can have at most arrows multi-digraph

The underlying mobility model

population of compartment in patch

Assume no birth or death. Balance inflow and outflow

when we write

The toy SLIRS model in patches

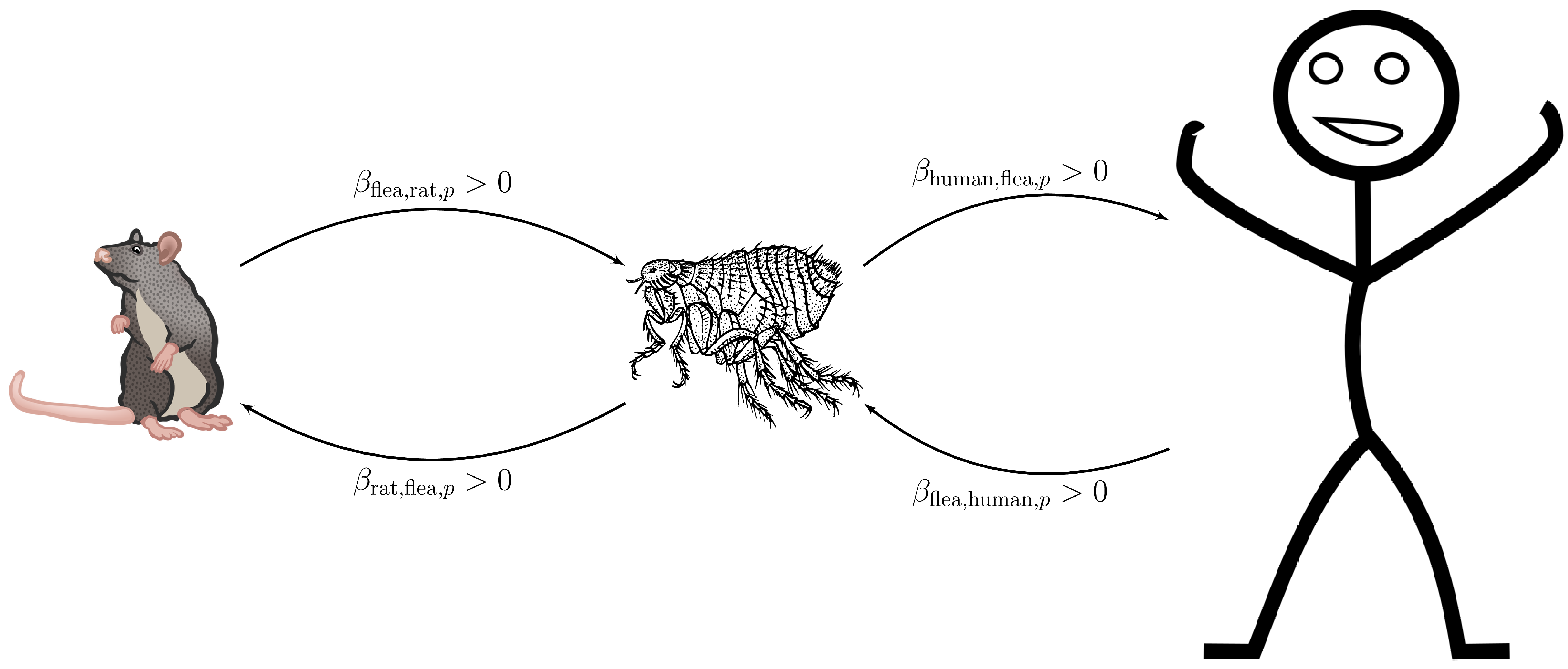
center

is the birth rate (typically or )

= latently infected ( exposed, although the latter term is ambiguous)

-SLIRS model

with incidence

-SLIRS (multiple species)

a set of species

with incidence

Oh, what a tangled web we weave

(Walter Scott, not Shakespeare)

Consider, e.g., with ,

  • describes intra- and inter-species possibilities of transmission in a location
  • If the encounter of a susceptible from species and an infectious from species in location can lead to infection of the susceptible then otherwise

Malaria and many vector-borne diseases

center

Plague (bubonic, not pneumonic)

center

center

-SLIRS (residency patch/movers-stayers)

with incidence

General metapopulation epidemic models

uninfected and infected compartments, and

For , and ,

where and

Basic mathematical analysis

Analysis - Toy system

For simplicity, consider -SLIRS with

with incidence

System of equations

Size is not that bad..

System of equations !!!

However, a lot of structure:

  • copies of individual units, each comprising 4 equations
  • Dynamics of individual units well understood
  • Coupling is linear

Good case of large-scale system (matrix analysis is your friend)

Notation in what follows

  • a square matrix with entries denoted

  • if for all (could be the zero matrix); if and with ; if . Same notation for vectors

  • spectrum of

  • spectral radius

  • spectral abscissa (or stability modulus)

  • is an M-matrix if it is a Z-matrix ( for ) and , with and

Behaviour of the total population

Consider behaviour of . We have

So

Vector / matrix form of the equation

We have

Write this in vector form

where -matrices with

The movement matrix

Consider a compartment . Then the following hold true:

  1. and corresponds to left eigenvector
  2. singular M-matrix
  4. irreducible has multiplicity 1

The nice case

Recall that

Suppose movement rates equal for all compartments, i.e.,

Then

Equilibria

given, of course, that (or, equivalently, ) is invertible.. Is it?

Perturbations of movement matrices

a movement matrix and a diagonal matrix. The following hold true:

  1. for all
  2. and is associated with an eigenvector . If, additionally, irreducible, then has multiplicity 1 and is associated with
  3. nonsingular M-matrix and
  4. irreducible and irreducible nonsingular M-matrix and

Nonsingularity of

Using a spectrum shift,

This gives a constraint: for total population to behave well (in general, we want this), we must assume all death rates are positive

Assume they are (in other words, assume nonsingular). Then is nonsingular and unique

Behaviour of the total population with equal movement

attracts solutions of

Indeed, we have

Since we now assume that is nonsingular, we have (spectral shift & properties of )

irreducible (provided , of course)

Behaviour of total population with reducible movement

Assume reducible. Let be the number of minimal absorbing sets in the corresponding connection graph . Then

  1. The spectral abscissa has multiplicity
  2. Associated to is a nonnegative eigenvector s.t.
    • if is a vertex in a minimal absorbing set
    • if is a transient vertex

From Foster and Jacquez, Multiple zeros for eigenvalues and the multiplicity of traps of a linear compartmental system, Mathematical Biosciences (1975)

The not-so-nice case

Recall that

Suppose movement rates similar for all compartments, i.e., the zero/nonzero patterns in all matrices are the same but not the entries

Let

and

Cool, no? No!

Then we have

Me, roughly every 6 months: Oooh, coooool, a linear differential inclusion!

Me, roughly 10 minutes after that previous statement: Quel con!

Indeed and are are not movement matrices (in particular, their column sums are not all zero)

So no luck there..

However, non lasciate ogne speranza, we can still do stuff!

Disease free equilibrium (DFE)

Assume system at equilibrium and for . Then and

Want to solve for . Here, it is best (crucial in fact) to remember some linear algebra. Write system in vector form:

where , -matrices ( diagonal)

at DFE

Recall second equation:

So unique solution if invertible.
Is it?

We have been here before!

From spectrum shift,

So, given , is the unique equilibrium and

DFE has

at the DFE

DFE has and , i.e.,

Recall: singular M-matrix. From previous reasoning, has instability modulus shifted right by . So:

  • invertible
  • nonsingular M-matrix

Second point (would have if irreducible)

So DFE makes sense with

Computing the basic reproduction number

Use next generation method with ,

Differentiate w.r.t. :

Note that

whenever , so

Evaluate at DFE

If , then

If , then

  • at DFE
  • at DFE

In both cases, block is zero so

Compute and evaluate at DFE

where . Inverse of easy ( block lower triangular):

where

as

Next generation matrix

where is block in . So

i.e.,

Local asymptotic stability of the DFE

Define for the -SLIRS as

Then the DFE

is locally asymptotically stable if and unstable if

From PvdD & Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission, Bulletin of Mathematical Biology 180(1-2): 29-48 (2002)

Global stability considerations

  • GAS is much harder
  • It has been done many times (look at my papers, but also those of Li, Shuai, Thieme, van den Driessche, Wang, Zhao..)
  • I am not aware of a way to do this generically

is not the panacea

An urban centre and satellite cities

JA & S Portet. Epidemiological implications of mobility between a large urban centre and smaller satellite cities. Journal of Mathematical Biology 71(5):1243-1265 (2015)

Context of the study

Winnipeg as urban centre and 3 smaller satellite cities: Portage la Prairie, Selkirk and Steinbach

  • population density low to very low outside of Winnipeg
  • MB road network well studied by MB Infrastructure Traffic Engineering Branch

Known and estimated quantities

City Pop. (2014) Pop. (now) Dist. Avg. trips/day
Winnipeg (W) 663,617 749,607 - -
Portage la Prairie (1) 12,996 13,270 88 4,115
Selkirk (2) 9,834 10,504 34 7,983
Steinbach (3) 13,524 17,806 66 7,505

Estimating movement rates

Assume movement rate from city to city . Ceteris paribus, , so . Therefore, after one day, , i.e.,

Now, , where number of individuals going from to / day. So

Computed for all pairs and of cities

Sensitivity of to variations of


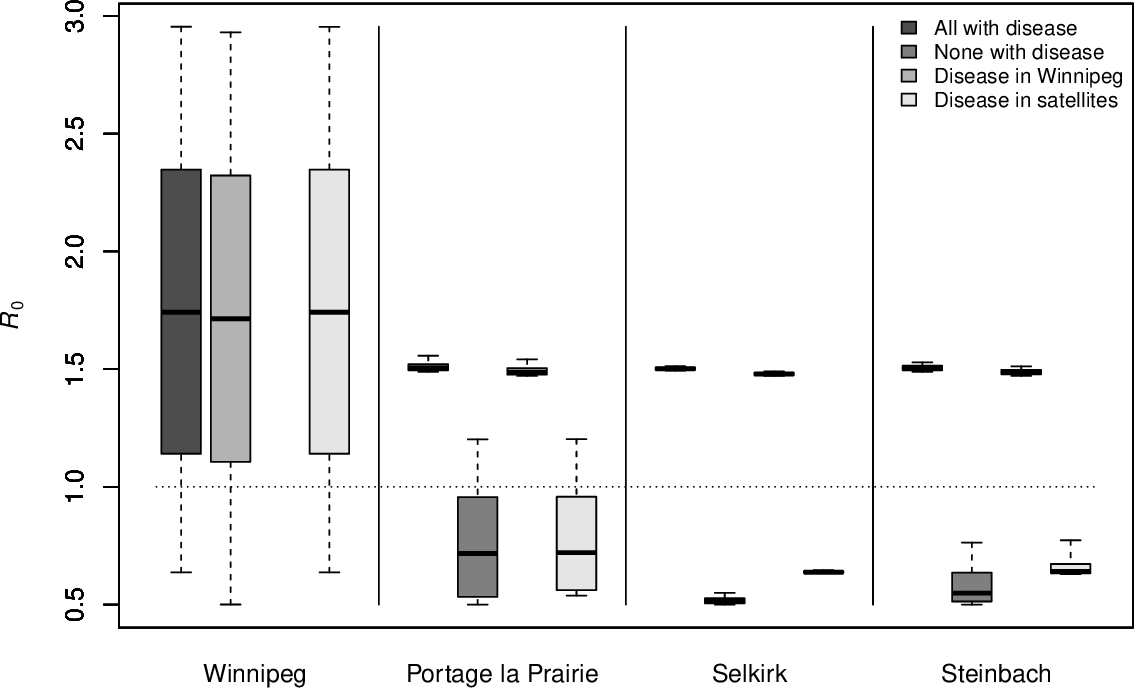
with disease: ; without disease: . Each box and corresponding whiskers are 10,000 simulations

Lower connectivity can drive

PLP and Steinbach have comparable populations but with parameters used, only PLP can cause the general to take values larger than 1 when

This is due to the movement rate: if , then

since is then block diagonal

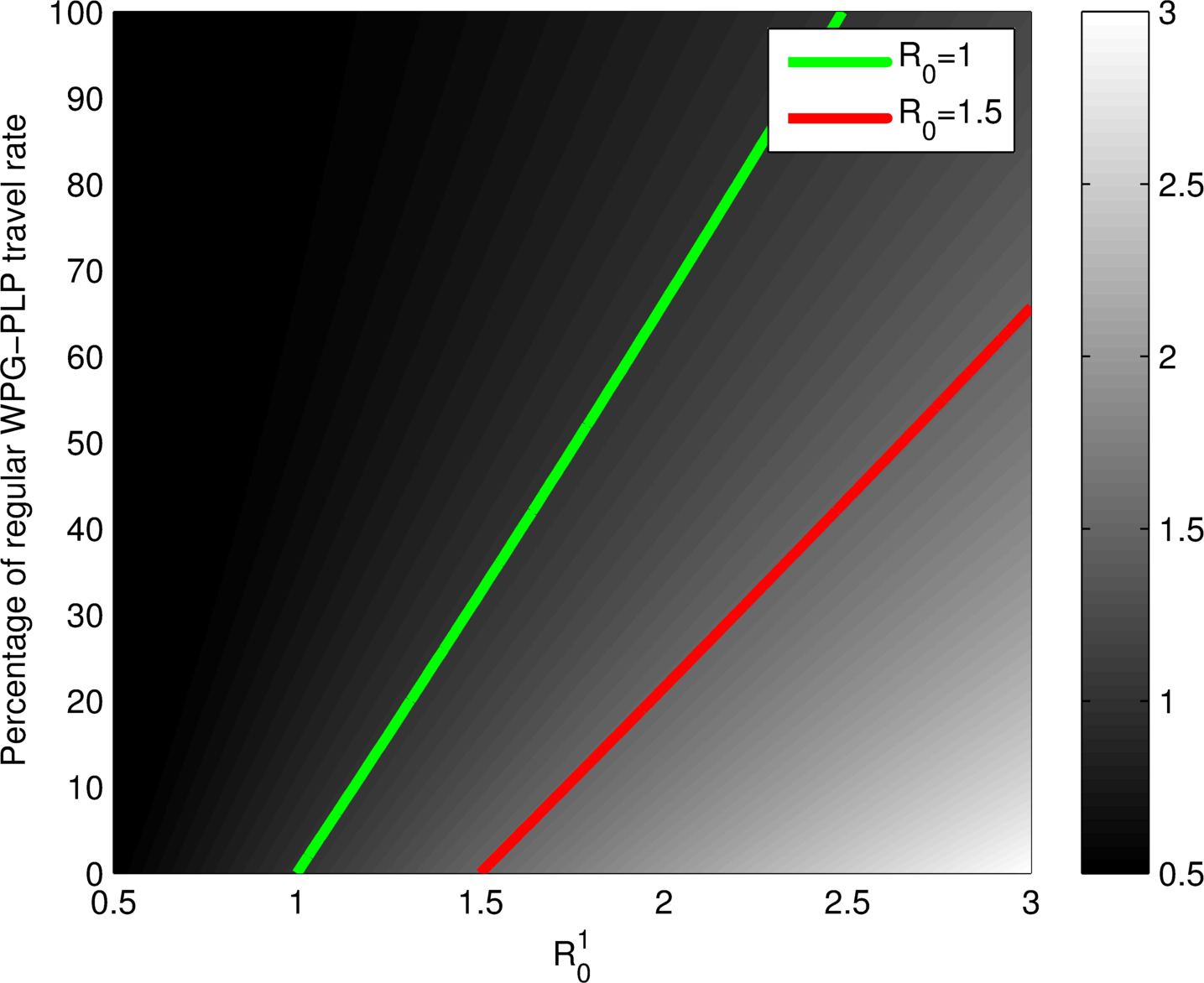
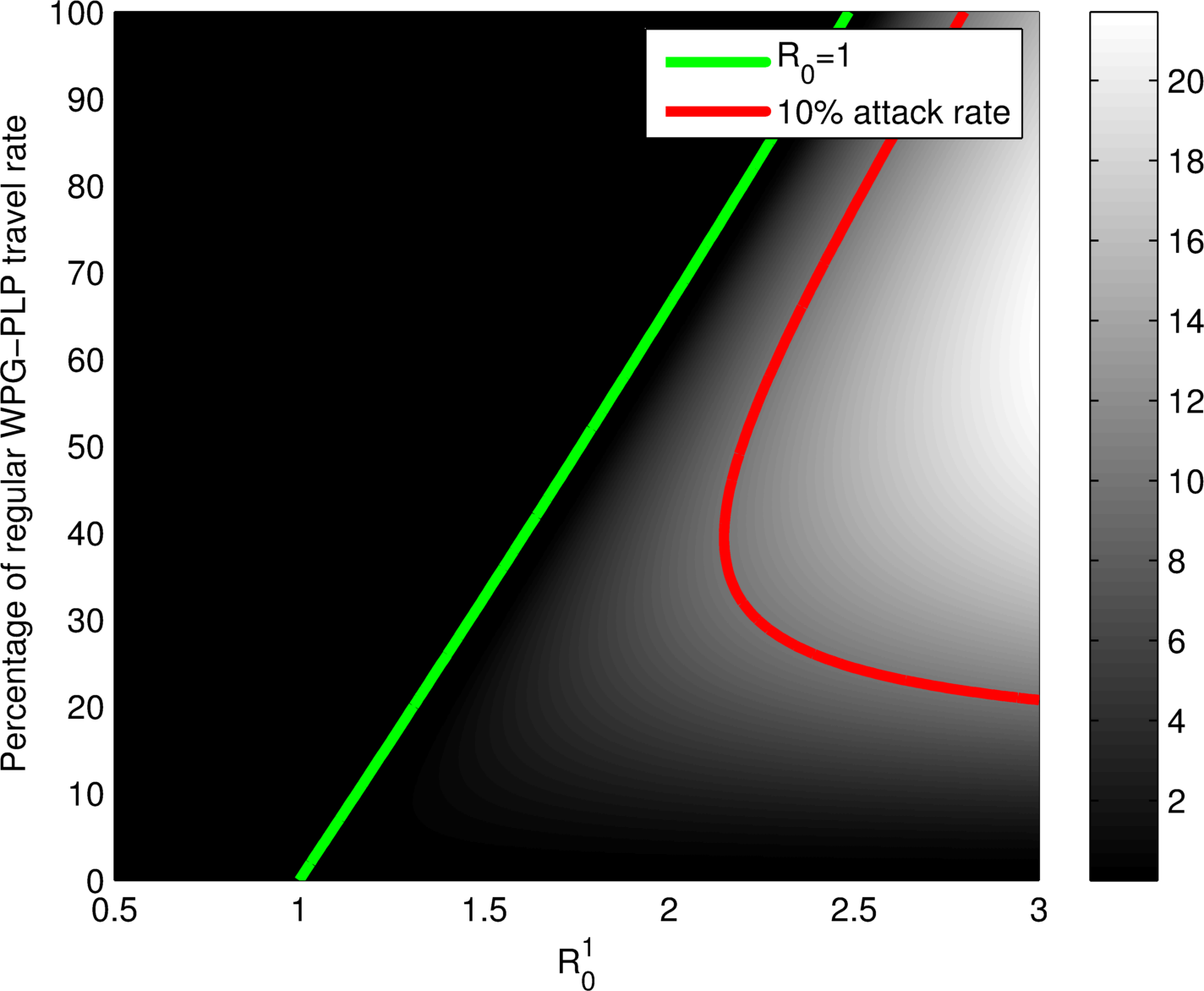
Movement rates to and from PLP are lower situation closer to uncoupled case and has more impact on the general

does not tell the whole story!


Plots as functions of in PLP and the reduction of movement between Winnipeg and PLP. Left: general . Right: Attack rate in Winnipeg

Problems specific to metapopulations

Inherited dynamical properties (a.k.a. I am lazy)

Given

with known properties, what is known of

  • Existence and uniqueness
  • Invariance of under the flow
  • Boundedness
  • Location of individual and general ?
  • GAS?

An inheritance problem - Backward bifurcations

  • Suppose a model that, isolated in a single patch, undergoes so-called backward bifurcations
  • This means the model admits subthreshold endemic equilibria
  • What happens when you couple many such consistuting units?

YES, coupling together backward bifurcating units can lead to a system-level backward bifurcation

JA, Ducrot & Zongo. A metapopulation model for malaria with transmission-blocking partial immunity in hosts. Journal of Mathematical Biology 64(3):423-448 (2012)

Metapopulation-induced behaviours ?

"Converse" problem to inheritance problem. Given

with known properties, does

exhibit some behaviours not observed in the uncoupled system?

E.g.: units have DFE GAS, 1 GAS EEP behaviour, metapopulation has periodic solutions

Mixed equilibria

Can there be situations where some patches are at the DFE and others at an EEP?

This is the problem of mixed equilibria

This is a metapopulation-specific problem, not one of inheritance of dynamical properties!

Types of equilibria

[Patch level] Patch at equilibrium is empty if , at the disease-free equilibrium if , where are some indices with and are positive, and at an endemic equilibrium if

[Metapopulation level] A population-free equilibrium has all patches empty. A metapopulation disease-free equilibrium has all patches at the disease-free equilibrium for the same compartments. A metapopulation endemic equilibrium has all patches at an endemic equilibrium

Mixed equilibria

A mixed equilibrium is an equilibrium such that

  • all patches are at a disease-free equilibrium but the system is not at a metapopulation disease-free equilibrium
  • or, there are at least two patches that have different types of patch-level equilibrium (empty, disease-free or endemic)

E.g.,

is mixed, so is

Suppose that movement is similar for all compartments (MSAC) and that the system is at equilibrium

  • If patch is empty, then all patches in are empty
  • If patch is at a disease free equilibrium, then the subsystem consisting of all patches in is at a metapopulation disease free equilibrium
  • If patch is at an endemic equilibrium, then all patches in are also at an endemic equilibrium
  • If is strongly connected for some compartment , then there does not exist mixed equilibria

Note that MSAC and for all

Interesting (IMHO) problems

More is needed on inheritance problem, in particular GAS part (Li, Shuai, Kamgang, Sallet, and older stuff: Michel & Miller, Šiljak)

Incorporate travel time (delay) and events (infection, recovery, death ..) during travel

What is the minimum complexity of the movement functions below

required to observe a metapopulation-induced behaviour?

Numerical investigations of large-scale systems

Not very difficult

  • As for the mathematical analysis: if you do things carefully and think about things a bit, numerics are not hard. Well: not harder than numerics in low-D
  • Exploit vector structure

Set up parameters

pop = c(34.017, 1348.932, 1224.614, 173.593, 93.261) * 1e+06
countries = c("Canada", "China", "India", "Pakistan", "Philippines")
T = matrix(data = 
             c(0, 1268, 900, 489, 200, 
               1274, 0, 678, 859, 150, 
               985, 703, 0, 148, 58, 
               515, 893, 144, 0, 9, 
               209, 174, 90, 2, 0), 
           nrow = 5, ncol = 5, byrow = TRUE)

Work out movement matrix

p = list()
# Use the approximation explained in Arino & Portet (JMB 2015)
p$M = mat.or.vec(nr = dim(T)[1], nc = dim(T)[2])
for (from in 1:5) {
  for (to in 1:5) {
    p$M[to, from] = -log(1 - T[from, to]/pop[from])
  }
  p$M[from, from] = 0
}
p$M = p$M - diag(colSums(p$M))

p$P = dim(p$M)[1]
p$eta = rep(0.3, p$P)
p$epsilon = rep((1/1.5), p$P)
p$pi = rep(0.7, p$P)
p$gammaI = rep((1/5), p$P)
p$gammaA = rep((1/3), p$P)
# The desired values for R_0
R_0 = rep(1.5, p$P)

Write down indices of the different state variable types

Save index of state variable types in state variables vector (we have to use a vector and thus, for instance, the name "S" needs to be defined)

p$idx_S = 1:p$P
p$idx_L = (p$P+1):(2*p$P)
p$idx_I = (2*p$P+1):(3*p$P)
p$idx_A = (3*p$P+1):(4*p$P)
p$idx_R = (4*p$P+1):(5*p$P)

Set up IC and time

# Set initial conditions. For example, we start with 2
# infectious individuals in Canada.
L0 = mat.or.vec(p$P, 1)
I0 = mat.or.vec(p$P, 1)
A0 = mat.or.vec(p$P, 1)
R0 = mat.or.vec(p$P, 1)
I0[1] = 2
S0 = pop - (L0 + I0 + A0 + R0)
# Vector of initial conditions to be passed to ODE solver.
IC = c(S = S0, L = L0, I = I0, A = A0, R = R0)
# Time span of the simulation (5 years here)
tspan = seq(from = 0, to = 5 * 365.25, by = 0.1)

Set up to avoid blow up

Let us take for patches in isolation. Solve for 

for (i in 1:p$P) {
  p$beta[i] = 
    R_0[i] / S0[i] * 1/((1 - p$pi[i])/p$gammaI[i] + p$pi[i] * p$eta[i]/p$gammaA[i])
}

Define the vector field

SLIAR_metapop_rhs <- function(t, x, p) {
  with(as.list(p), {
    S = x[idx_S]
    L = x[idx_L]
    I = x[idx_I]
    A = x[idx_A]
    R = x[idx_R]
    N = S + L + I + A + R
    Phi = beta * S * (I + eta * A) / N
    dS = - Phi + MS %*% S
    dL = Phi - epsilon * L + p$ML %*% L
    dI = (1 - pi) * epsilon * L - gammaI * I + MI %*% I
    dA = pi * epsilon * L - gammaA * A + MA %*% A
    dR = gammaI * I + gammaA * A + MR %*% R
    dx = list(c(dS, dL, dI, dA, dR))
    return(dx)
  })
}

And now call the solver

# Call the ODE solver
sol <- ode(y = IC, 
           times = tspan, 
           func = SLIAR_metapop_rhs, 
           parms = p,
           method = "ode45")

One little trick (case with demography)

Suppose demographic EP is

Want to maintain for all to ignore convergence to demographic EP. Think in terms of :

So take

Then

and thus if , then and thus for all , i.e., for all

Word of warning about that trick, though..

has nonnegative (typically positive) diagonal entries and nonpositive off-diagonal entries

Easy to think of situations where the diagonal will be dominated by the off-diagonal, so could have negative entries

use this for numerics, not for the mathematical analysis

Epilogue / Postlude

In conclusion

  • Space is a fundamental component of the epidemic spread process and cannot be ignored, both in modelling and in public health decision making

  • One way to model space is to use metapopulation models

  • Metapopulation models are easy to analyse locally, give interesting problems at the global level

  • Simulation (deterministic and stochastic) can be costly in RAM and cycles but is easy

  • Metapopulation models are not the only solution! (see network models, individual-based models, ..)

Merci / Miigwech / Thank you

<div style = "text-align: justify">

</div>

<p style="margin-bottom:-1.5cm;"></p>